Future value annuity: Grade 12 finance
- Ramta Solutions
- Oct 7, 2018
- 3 min read
In this article, we assume you are well informed with the knowledge of geometric series.
When dealing with future value annuities, we are expecting capital growth by means of regular equal payments made into an investment account which grows at an intetest, i.
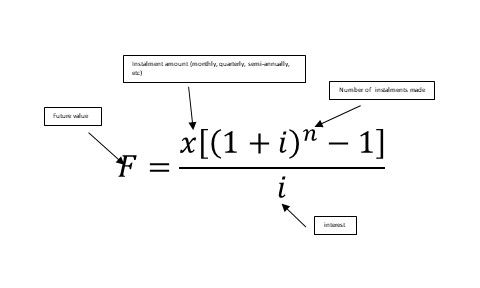
The above equation represents the formulation of the future value annuity. It is applied only when investment is made without deferment. This is used for an investment which is made by depositing (equally so) at the end of a term( monthly, quarterly, semi-annually, yearly, etc.).
Special case 1: payments made immediately
The equation above is used when installments are made at the end of a term. Now, we consider when an investment is made immediately. This would mean, if you do a timeline, your deposit starts at T0 and ends at T(n-1)[not at Tn]. It means, one invests at the beginning of a term.
The equation for this situation is given below.
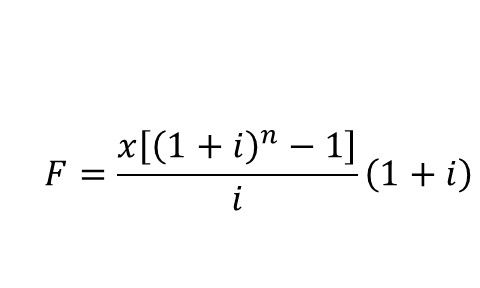
The RHS of the above equation is a product investment made at the end of the term(discussed above) and the (1+i) term attached to it. The (1+i) term is here because the account (objective of the account) is meant to cease at Tn and thus, all the money at T(n-1) grows with (1+i) at Tn.
NOTE: If installments stopped two terms before the expected last date, (1+i) will be raised to two. If stopped three terms before, it'll be raised to three, etc.
Special case 2: payments made immediately and thereafter at the end of a term
In the opening image, we discussed n as the number or installments made. The case of immediate payment and thereafter payments made at the end of a term, really brings justice to the definition above.
In this case, we will realise that we have an additional payment. To account for it, we add 1 to the n term of the equation. Look at the figure below.

We hope this small discussion helped. Now consider the following examples
Example
You want to invest for an overseas vacation after seven months of employment, so you open an investment account and the bank say they offer interest of 12% p.a. compounded monthly. You made your first payment immediately and thereafter defaulted for two months. You then made five equal payments of R5 000 per month. How much would you have after seven months?
Solution:
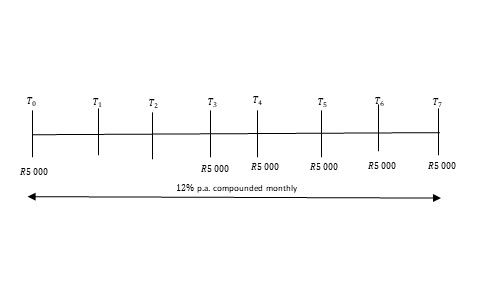
The solution to this question is two part.
The first part is that the R5 000 made at T0 will not qualify to be used for the future value annuity. Therefore we will use the accumulated amount definition and let n equal 7.
The second part exhibits the condition of the future value annuity when instalments are made at the end of a term. For this part, n is five.
The solution therefore involves the answers of both parts. Try see if you get R30 865.70
2. Tumelo is investing for a warehouse after 10 years. He makes monthly payment of R7 500 to an account paying interest of 13.25% p.a. compounded monthly. How much will he have after 10 years.
Get your answer as R 1 857 711.70 (You used the equation as it is)
3. As is the case above, he makes his last payments at the 117th instalment. How much will he have after 10 years
Your answer is R1 834 962.35
To get help on these and more, click here to request for a tutor near you








Comments